image depicting Robert Krook, a functional programmer based in Gothenburg

Robert Krook

Front page / Posts

QuickerCheck

Why Parallel QuickCheck

I recently did some fun work on compiler testing together with Bo Joel Svensson and Koen Claessen, using QuickCheck (QC), and lamented over how slow my tests executed. When using QC to test a compiler there are really a lot of things happening at once. Every test has to

Naturally, doing all of this takes some time. We are talking seconds rather than minutes, but still enough time that running a reasonable amount of tests takes a non-trivial amount of time. All my tests are independent, so it made sense that I should be able to run them in parallel. Yet, QC has no support for this.

In some settings it does not make sense to introduce parallelism. In Python, for example, the authors of the Hypothesis library does not support parallelism. They do not know what functions they are wrapping, and parallelism may introduce problems such as race conditions. In Haskell, this is not as much of a problem. We are used to splitting up our code in its pure and effectful parts. Even effectful code might be threadsafe, or can easilly be made so.

How does QuickCheck work?

Without going into too many of the gory details, this is roughly how the testing loop work.

The test loop is parameterised over a state. This state contains information that the testing loop requires to operate, such as the random seed to use for generating the next test case, statistics of how many tests we ran so far, and statistics we might have instructed our property to collect (labels and such).

While individual tests may be emberrasingly parallel, the test loop actually imposes an order to tests, as a result of how QC computes sizes for your test case. QC tries to first generate small test cases, and then gradually increases them as you pass more and more tests. The size grows from 0 to maxSize (configurable), before it wraps around and begins anew. This is implemented by deriving a size from the number of tests that you have passed so far (note: passed, not run).

Look at the generator for lists

listOf :: Gen a -> Gen [a]
listOf g = sized $ \size -> do
  n <- chooseInt (0, size)
  vectorOf n g

The generator begins by drawing upon the size parameter supplied by QC, using the sized function, and then generates a number between 0 and the size. It then proceeds with generating a list of that length, using the supplied generator to generate the individual elements.
What we should take away from this is that when we begin testing, and the size is zero, we can only generate the empty list.

Now, consider the property below

prop :: [Int] -> Property
prop xs = not (null xs) ==> xs

This property generates arbitrary lists of integers, but only proceeds to test the property if the list is not empty. If an empty list is generated, the list is discared and QC generates a new one. However, we have still passed the same number of tests, so the computed size is the same. This means that in the case of the first test we ever run, we have no way of generating a non-empty list. How does QC deal with this?

It is simple, but wonky. QC computes the size for a test case based not just on the number of tests that passed, but also on the number of tests that has been discarded in a row. When a magic number of 10 test cases have been discarded, the size is increased by one. Now we can generate lists of length either 0 or 1, and can test the property. Simplified, the function looks something like this

computeSize :: Int -> Int
computeSize numPassed numDiscarded = numPassed `mod` maxSize + (numDiscarded `div` 10)

There is some more things going into this to handle corner cases etc, but this is the important bit.
This way of computing sizes results in a data dependency. We can not compute the size for the ith test before we have run and observed the output of the first (i-1) tests. Without knowing how many tests we have passed in total, and how many tests we have recently discarded, we can not compute the size for the next test. Running tests in parallel immediately became significantly trickier, because we do not know what sizes we should use for concurrent tests.

What does QuickerCheck do?

QuickerCheck does a best effort attempt at running tests using the same sizes that would have been used, had they been run sequentially. QuickerCheck run several instantiations of the sequential testing loop in parallel, each thread managing a testing state of their own. Each concurrent tester will compute the size for its next test based on its own thread-local state (how many tests this thread passed or discarded so far), and a stride. The stride will make sure that all testers together explore an approximation of the set of sizes that we would have, had we run the tests sequentially.
Once a bug is found, QuickerCheck is able to shrink it in parallel. It will spawn concurrent shrinkers that essentially try to find the next counterexample from the current shrink candidates.

The code can be found here: https://github.com/Rewbert/quickcheck there are some hacks in place that are not meant to stay, so if you see something particularly wonky, do not worry. My usage of asynchronous exceptions, for example, is particularly wonky.
The paper can be found here: quickercheck.pdf

Will it be merged?

Yes, the plan is to hopefully merge this in the next breaking change of QC, 2.16. There is no timeframe for when this will happen, but I expect it to take a while. One module in particular (Features.hs) is completely commented out, and has to be restored before anything can be merged. Not only does this work introduce a lot of changes to QC, it will break other packages that depend on QC (for example Tasty and hspec). Before any merge happens there must be a strategy for solving these problems so that there are no disruptions in the ecosystem. Furthermore, what I have implemented may change a lot before it makes its way into QC. So far I am the only developer that has laid eyes on this code, which is usually not a good thing.

How can I try it out until then?

You can already try it out with very little effort, thankfully. The steps are

  1. Since it is not posted on hackage as a separate package you will need to redirect your project to fetch QuickCheck from my fork. You can do this by either editing your current cabal.project file, or creating a new one, and inserting 
    source-repository-package
  type: git
  location: https://github.com/Rewbert/quickcheck.git
  -- optionally also add this to point to a particular commit, otherwise you will always get the freshest master commit
  -- tag:
    This makes cabal look for the QuickCheck package on my github, rather than hackage.

  2. You need to add some extra flags when you build your project. Nothing goes wrong if you forget to use them, but your tests will not be multithreaded.
    If you use cabal, you can add these to your .cabal-file

    ghc-options: -threaded -feager-blackholing -rtsopts

  3. You now need to modify your code. It is enough to change your call to quickCheck with a call to quickCheckPar.

  4. Finally, when you run your program, you need to pass in a runtime option that tells the runtime how many schedulers to create. You do this by running your cabal project like this

    cabal run my-exe -- +RTS -N[n]

    where the last [n] can be either omitted completely (at which point GHC will fetch the number from your machine), or given by you, specifying exactly how many schedulers to use.

Nothing in the existing QC API has been changed, so it should be a very simple drop-in replacement. The API is, however, extended. There are new top-level invocation methods quickCheckPar, quickCheckParResult, quickCheckParWith, quickCheckParWithResult. These functions query the runtime system for how many HECs there are, and spawn that many workers.

The other bigger extension is that there are a few new flags that can be configured in the Args type. The new flags are

Also remember that all your workers will share the available resources. This includes much more than simply the pool of processors, but also RAM, caches, disk space, etc. Also, the paper goes into some more detail of how workers are aborted, and how we can recover from that gracefully, etc.

Results

Below follow some of the results presented in the paper. Unless otherwise stated, all results are collected with the chatty flag set to False.
The first thing we might want to know is whether we pay any performance penalty by using the new runtime sequentially. That is, if we are not interested in parallel testing, does our sequential tests get slower? A full description of the different benchmarks below can be found in the paper.

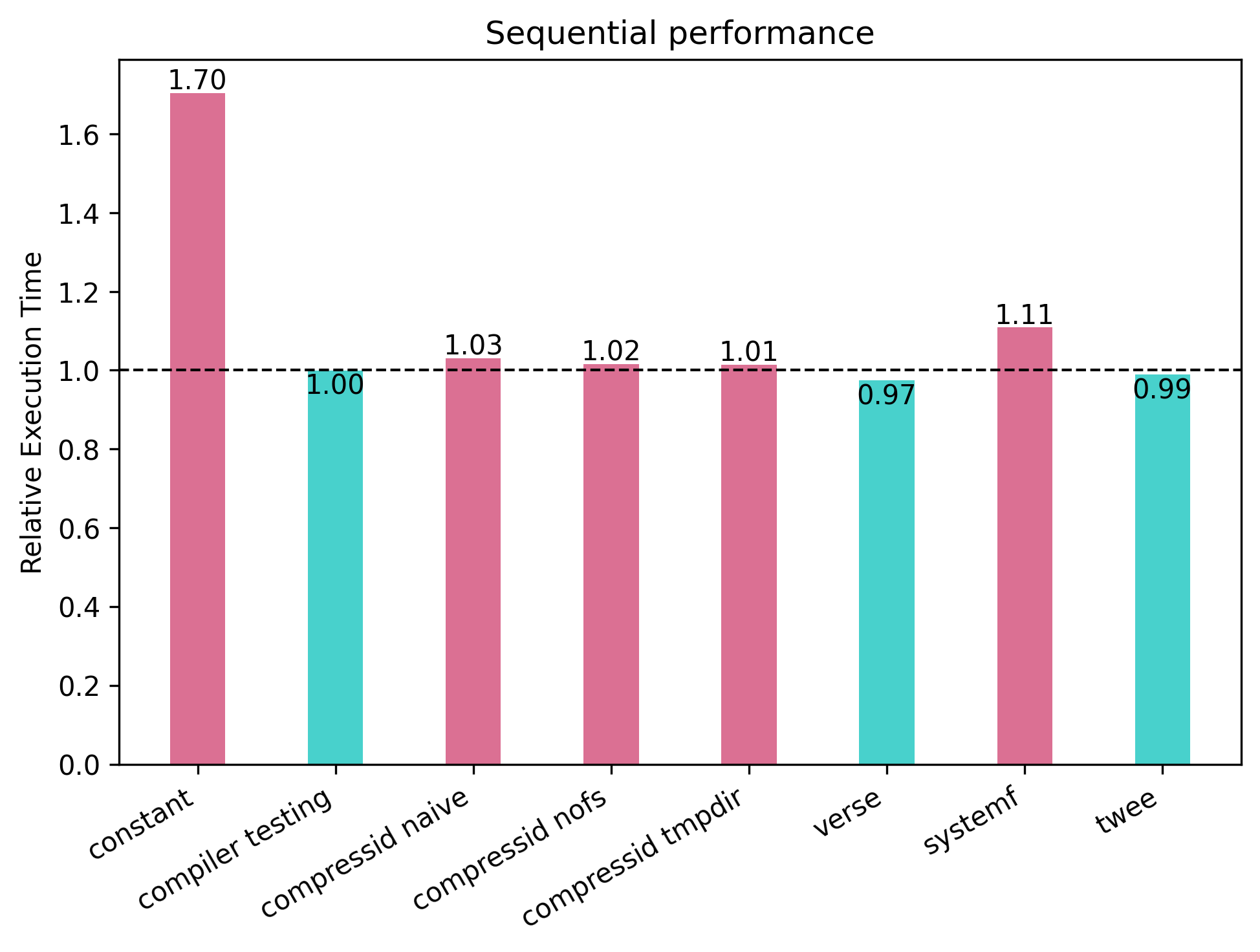
In general it appears that there is not much difference. Some tests are faster, and some are slightly slower. A number of 1 means that QuickerCheck required exactly as much time as QC to complete the same task. A number greater than 1 means that QuickerCheck was slower and required more time.
The constant benchmark is intended to measure the worst case behavior. It is a property that does nothing, meaning that it spends all its time inside the test loop itself, and it was around 70% slower. All the other benchmarks actually do some work, and have much more modest changes in performance. From these measurements I would conclude that you don't pay any noticeable penalty from using the new testing loop with just one core.

Now, what if we add more cores. How much speedup do we gain?

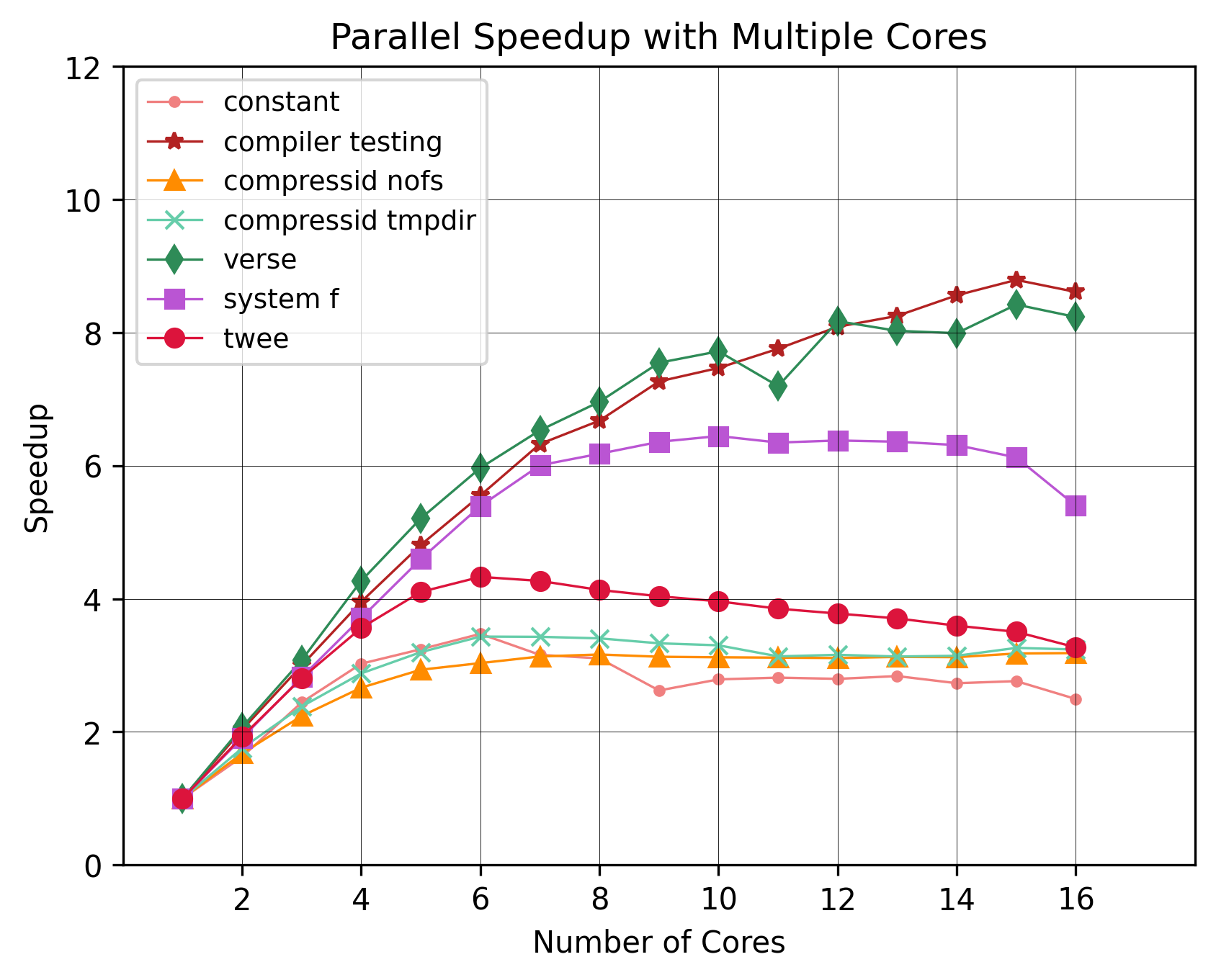
Up until the point where we exhaust our physical cores, we have quite a nice speedup. After that we can see that acceleration slows down. Some benchmarks saw more than an 8x speedup, whereas others saw a more moderate 4x-6x speedup. Even the outlier constant saw a 3x speedup.

QC is all about finding bugs. Can we find bugs faster? We evaluate this by planting a single bug in four of the benchmarks, and measure how long it takes for us to find it. We do this several hundred times per core configuration, and take the median of those numbers.

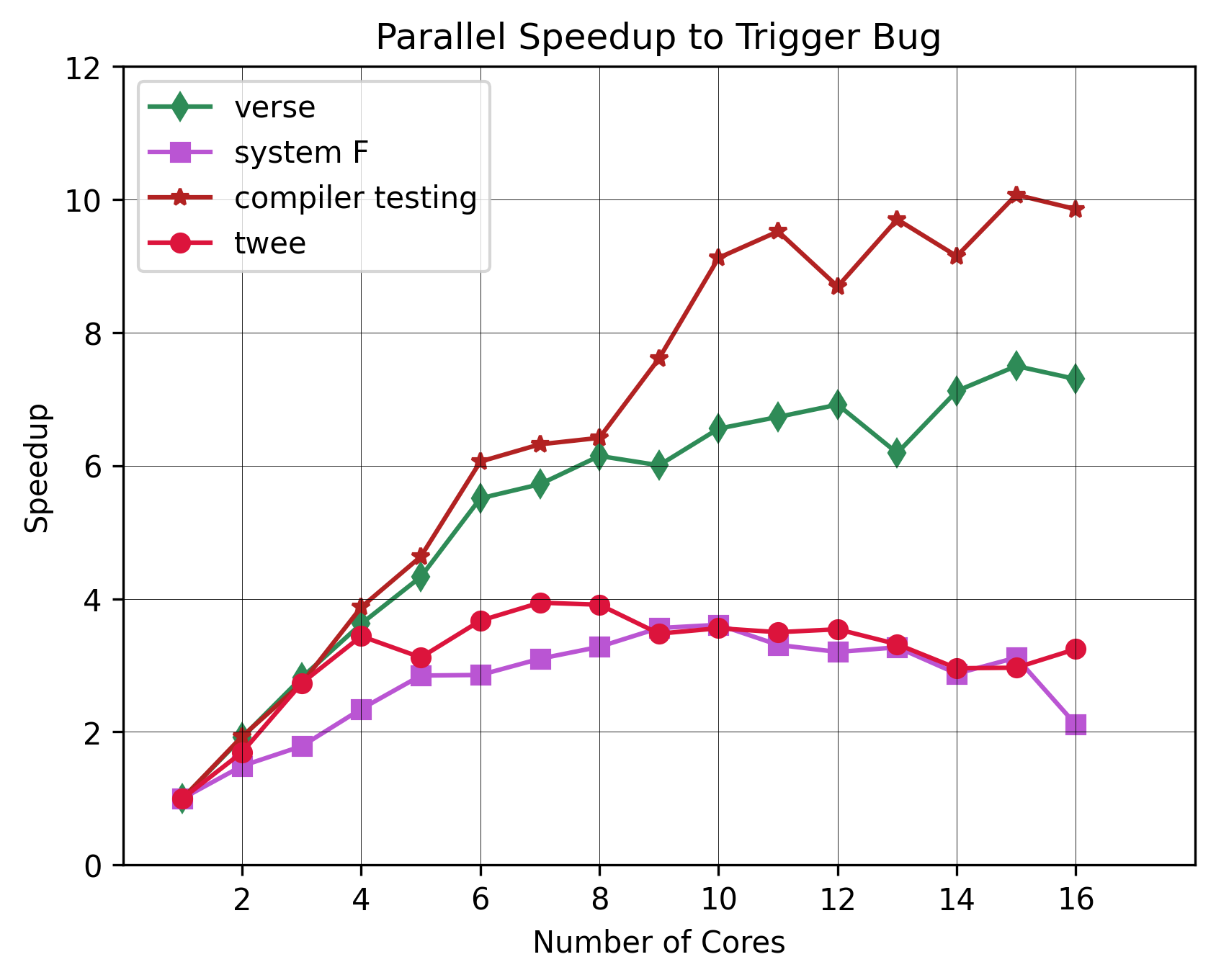
The results show that we do, indeed, find the bugs faster. There is no number of cores we can use that would give us a slower time than the sequential one. The maximum speedup was roughly 10x for the compiler testing benchmark.

Lastly, what about the quality of shrunk counterexamples? If we shrink them in parallel, we may end up with a different counterexample than the one we would have found had we shrunk it sequentially. We evaluate this by computing the size of a counterexample (number of constructors in the term). We assume that the sequential sizes are drawn from a ground truth distribution, and try to model the sizes collected using more cores as another distribution. We compute the difference between these distributions and try to say whether they are equal or not. In the figure we refer to the sequential distribution as the deterministic one, and refer to the parallel one as the greedy one. We only render the results where the specific choice of number of cores yielded the largest difference in distributions (i.e the worst results). We do this for two benchmarks, the compiler testing one and the verse one.

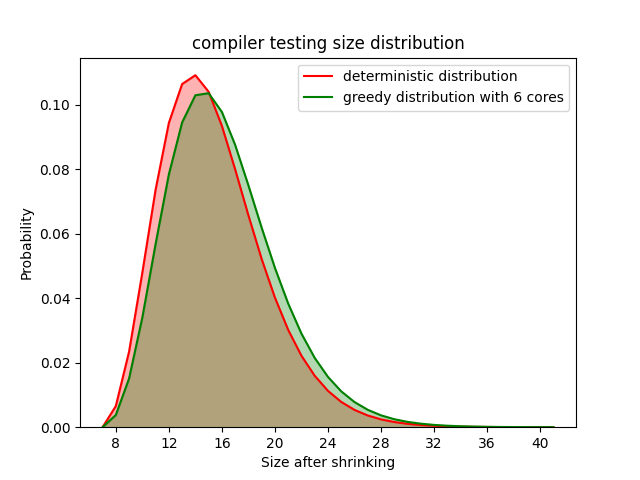
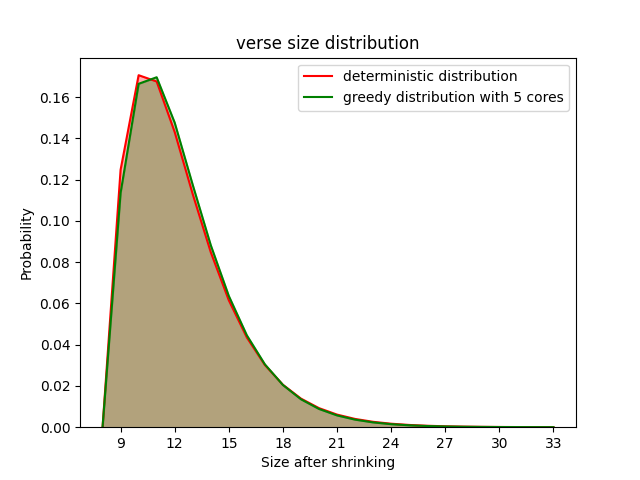
Ofcourse the quality of the shrinker plays a role in these results, and these shrinkers were written by domain experts. From these results it seems as if the quality (sizes) of shrunk counterexamples is not largely affected by the choice of algorithm. If the parallel shrinker is faster, there does not seem to be any problems with using it.

Are there bugs?

Certainly. If you find any, please open an issue on my fork of QuickCheck, or send me an email at krookr@chalmers.se.